深海裝備技術(shù)是未來世界各國爭奪戰(zhàn)略制高點的關(guān)鍵，已成為目前國際深海科學(xué)最前沿的研究領(lǐng)域。 作為深海資源探測與開發(fā)不可缺少的技術(shù)裝備，深海潛水器越來越多地引起世界各國的關(guān)注。在深海潛水 器眾多子系統(tǒng)中，耐壓結(jié)構(gòu)承受周圍海水壓力載荷[1-2]，保護內(nèi)部人員生命安全以及保障儀器設(shè)備正常工作， 是潛水器的核心系統(tǒng)。針對耐壓結(jié)構(gòu)的安全性評估，傳統(tǒng)方法主要考慮靜強度、極限載荷和疲勞 3 個方 面[3-5]。在深海環(huán)境下工作的耐壓結(jié)構(gòu)外表面承受著極高的靜水載荷，當耐壓結(jié)構(gòu)外殼的應(yīng)力超過屈服強 度、屈曲強度或抗拉強度時會發(fā)生內(nèi)爆。耐壓結(jié)構(gòu)在內(nèi)爆過程中被壓潰塌陷，當水流壓縮結(jié)構(gòu)至極限時會 發(fā)生水錘型沖擊，水流動能轉(zhuǎn)化為沖擊波的能量對周圍結(jié)構(gòu)造成破壞。2014年美國全海深無人潛水器“海 神”號（圖1）于水下9.9 km左右處發(fā)生內(nèi)爆，整個潛器蕩然無存，所有設(shè)備幾乎成為碎片[6]。其原因并非單個 耐壓結(jié)構(gòu)發(fā)生的內(nèi)爆現(xiàn)象，而是搭載的1 472個陶瓷耐壓結(jié)構(gòu)出現(xiàn)了連鎖內(nèi)爆（殉爆），導(dǎo)致數(shù)倍于環(huán)境壓力 的沖擊波鏈式傳遞，直至潛器損毀。2017年阿根廷海軍“圣胡安”號（圖2）潛艇失事，沉入約0.9 km深海底， 整個艇體承受巨大水壓作用內(nèi)爆而解體[7]。2023年加拿大“泰坦”號（圖3）載人潛水器在北大西洋約3.8 km深處觀察“泰坦尼克”號殘骸時失聯(lián)，隨后發(fā)生“災(zāi)難性內(nèi)爆”。可見，深海環(huán)境下耐壓結(jié)構(gòu)內(nèi)爆必須引起 重視。

水下內(nèi)爆的研究最早可以追溯到1917年Rayleigh[8]在理想流體假設(shè)基礎(chǔ)上推導(dǎo)了氣泡潰滅速度和內(nèi)部 壓力。此后 Plesset[9]在 Rayleigh 工作的基礎(chǔ)上進一步考慮了流體的黏性和表面張力，得到了經(jīng)典的氣泡動 力學(xué)方程。Keller-Miksis[10]方程則進一步引入了氣泡界面運動馬赫數(shù)，考慮了流體可壓縮性對氣泡潰滅的 影響。后來眾多學(xué)者又針對多氣泡相互作用理論模型開展了相關(guān)研究，Zhang等[11]建立了統(tǒng)一氣泡方程，可 以同時考慮氣泡相互作用、邊界效應(yīng)、遷移效應(yīng)等綜合影響，在內(nèi)容上統(tǒng)一了經(jīng)典的 Plesset-Rayleigh 方程、Keller-Miksis方程和Gimore[12]方程等，在理論上能夠更加準確地預(yù)測氣泡的坍塌行為。

盡管氣泡在水下的坍塌和潰滅與耐壓結(jié)構(gòu)內(nèi)爆存在一定的相似性，但是由于耐壓結(jié)構(gòu)坍塌變形過程中 的隨機性，且金屬耐壓結(jié)構(gòu)存在顯著的吸能特性，導(dǎo)致深海耐壓結(jié)構(gòu)水下內(nèi)爆與氣泡動力學(xué)存在一定的差 異，因此有必要開展深海耐壓結(jié)構(gòu)水下內(nèi)爆的研究。美國海軍[13-14]2004年發(fā)布的無人潛水器計劃也要求潛水器的設(shè)計必須嚴格考慮耐壓結(jié)構(gòu)內(nèi)爆所產(chǎn)生的影響。中國早在20世紀80年代就開展了耐壓結(jié)構(gòu)的水下 內(nèi)爆研究，上海交通大學(xué)水下工程研究所朱繼懋課題組[15-18]針對內(nèi)爆對壓力筒試驗裝置的潛在威脅，開展了 系列化數(shù)值計算研究。近些年針對“海神”號陶瓷耐壓結(jié)構(gòu)的水下內(nèi)爆也開展了許多的研究，Zhang等[19]通 過計算機斷層掃描技術(shù)獲得了陶瓷球真實的幾何形狀，再進行有限元仿真分析了陶瓷球在內(nèi)爆臨界狀態(tài)的 失效過程，認為陶瓷球的失效是由內(nèi)表面過大的局部拉應(yīng)力引發(fā)。Sun和Zhao[20]、Sun等[21]采用可壓縮多相 流方法結(jié)合自適應(yīng)網(wǎng)格技術(shù)，探究了萬米級陶瓷球水下鏈式內(nèi)爆特性，并分析了不同空間位置陶瓷球鏈式 內(nèi)爆的聚攏效應(yīng)。Hu等[22]采用耦合的歐拉-拉格朗日（coupled Eulerian-Lagrangian， 簡稱CEL）方法研究了在 不同靜水壓力下由沖擊、擠壓以及初始缺陷引發(fā)的陶瓷球內(nèi)爆，提出內(nèi)爆沖擊波和結(jié)構(gòu)破裂過程緊密相關(guān)。

Gish和Wierzbicki[23]在壓力罐中進行了水下金屬圓柱殼的內(nèi)爆試驗，分析了圓柱殼長度、直徑和厚度對 沖擊波的影響。Turner[24]、Turner和 Americo[25]首先開展了玻璃球的水下內(nèi)爆試驗，得到了內(nèi)爆過程的壓力 時程曲線，并通過仿真與試驗結(jié)果的對比，強調(diào)不能忽略球殼結(jié)構(gòu)對內(nèi)爆過程的影響；之后又對鋁合金薄壁 圓管進行了一系列小規(guī)模水下內(nèi)爆試驗，同時進行數(shù)值模擬對圓管內(nèi)爆過程中壓力脈沖的演化特征進行了 詳細分析。Gupta等[26]使用3D數(shù)字圖像技術(shù)研究了靜水環(huán)境中圓柱管內(nèi)爆的物理過程，該研究可視化了圓 柱管的實時變形，同時對其中的流固耦合現(xiàn)象進行了分析。Wei等[7]通過數(shù)值模擬還原了阿根廷“ 圣胡安” 號潛艇內(nèi)爆的整個過程。Zheng等[27]、Zheng和 Zhao等[28]基于有限體積法自行開發(fā)了可壓縮多相流求解模 塊，采用任意拉格朗日歐拉（arbitrary Lagrangian-Eulerian，簡稱ALE）方法研究了深海鈦合金耐壓結(jié)構(gòu)的水下 內(nèi)爆毀傷特性，并開展了鈦合金耐壓結(jié)構(gòu)水下內(nèi)爆流固耦合試驗，探究了不同環(huán)境水深下薄壁鈦合金耐壓 結(jié)構(gòu)的水下內(nèi)爆特征。

然而隨著人類向深海探索的深入，潛水器下潛深度也越來越大，長期使用和反復(fù)上浮下潛的作業(yè)需要、 極端的深海壓力以及復(fù)雜的海域工況等，對耐壓結(jié)構(gòu)材料的安全性和可靠性提出了更高要求。鈦合金材料 由于具有輕質(zhì)、高比強度、良好的冷熱成型能力以及優(yōu)異的抗海水腐蝕性能，因而在深海潛水器中的應(yīng)用越 來越廣泛[29]。然而，鈦合金抗拉強度與屈服強度接近，塑性變形范圍較窄，一旦出現(xiàn)可導(dǎo)致大變形的極端載 荷，結(jié)構(gòu)就會產(chǎn)生破壞，潛水器在大深度海水中的生存狀況將會異常危險。文章采用 LS-DYNA 軟件中的ALE方法，開展大深度環(huán)境下鈦合金耐壓結(jié)構(gòu)的內(nèi)爆現(xiàn)象以及損傷失效機理研究，分析鈦合金耐壓結(jié)構(gòu)內(nèi) 爆時的流固耦合機制、結(jié)構(gòu)動態(tài)響應(yīng)及能量演化機理，探究超大深度載荷下鈦合金耐壓結(jié)構(gòu)極限強度失效 破壞的物理機制，并對比了不同球殼半徑以及不同環(huán)境水壓對內(nèi)爆過程中能量轉(zhuǎn)化、結(jié)構(gòu)變形失效以及流 場特性的影響。

1、數(shù)值方法

1.1　可壓縮兩相流控制方程

深海鈦合金耐壓結(jié)構(gòu)水下內(nèi)爆時間極短，流體運動速度極大，且伴隨著巨大的能量聚集和釋放，是一個 高雷諾數(shù)流動，因此忽略流體黏性的同時需要考慮水-氣兩相流的可壓縮性。深海耐壓結(jié)構(gòu)水下內(nèi)爆過程中 可壓縮兩相流的質(zhì)量、動量和能量守恒控制方程分別為：

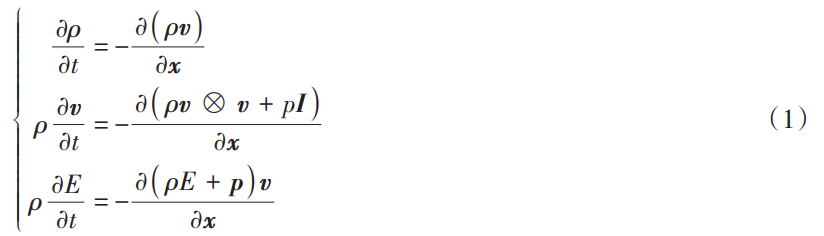
式中：t為時間；x為空間位置；v為流體速度矢量；ρ為材料密度；p為流體壓強；I為單位向量；E為物質(zhì)的總能 量；⊗表示矢量外積。 為了封閉上述可壓縮多相流控制方程，水采用Grüneisen狀態(tài)方程[30]進行描述：

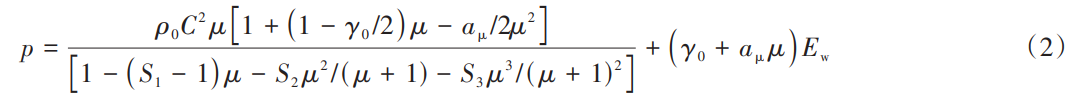
式中：ρ0為水在常溫狀態(tài)下的初始密度，取 1 000 kg/m3；C 為水中的聲速，取 1 490 m/s；μ 為水的壓縮比，μ =ρ/ρ0 - 1；γ0為Grüneisen系數(shù)，取1.65；aμ為相應(yīng)的修正系數(shù)，取0；S1 、S2 、S3為us-up曲線斜率的無量綱系數(shù)，S1=1.79，S2=S3=0；Ew為水的單位體積內(nèi)能。

空氣采用線性多項式狀態(tài)方程[30]進行描述：

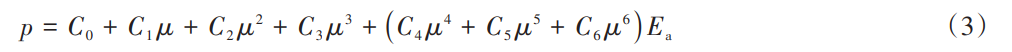
式中：線性多項式狀態(tài)方程系數(shù)C4=C5=0.403，其余均為0；Ea為空氣的單位體積內(nèi)能。

1.2　流固耦合方法

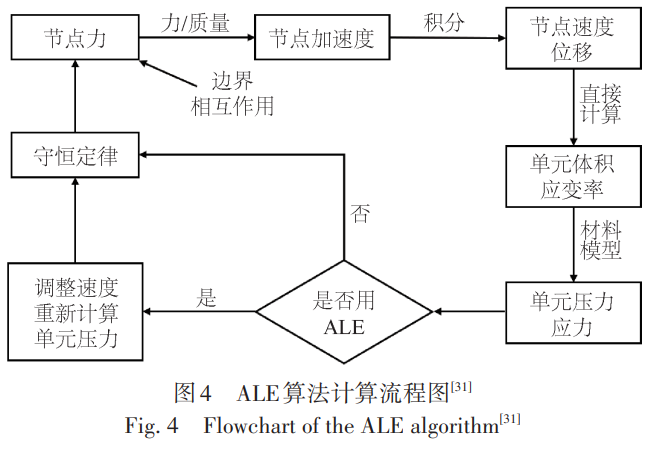
采用ALE方法進行深海鈦合金耐壓結(jié)構(gòu)水下內(nèi)爆動態(tài)響應(yīng)機理研究時，首先通過一個或多個Lagrange時間步計算跟蹤物質(zhì)邊界的運動；然后執(zhí)行ALE時間步計算，并根據(jù)變形后的物體邊界，保持原來的拓撲關(guān) 系對內(nèi)部單元重新劃分網(wǎng)格；最后將變形網(wǎng)格中的單元變量以及節(jié)點速度矢量輸運到重分后的新網(wǎng)格 中[31]。圖4為進行水下內(nèi)爆流固耦合數(shù)值計算中ALE算法的計算流程圖。

ALE算法中還需要引入除Lagrange坐標系和Euler坐標系之外的一個參考坐標系，在該坐標系下物質(zhì)的 時間導(dǎo)數(shù)可以通過鏈式法則[27]得到：

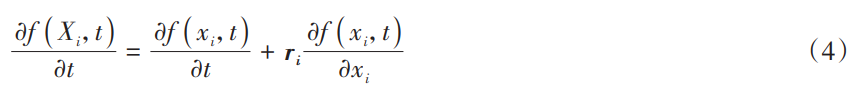
式中：Xi和xi分別為Lagrange坐標和Euler坐標點；假設(shè)流體速度為vi，網(wǎng)格速度為wi，則流體質(zhì)點和網(wǎng)格之間 的相對速度可表示為 ri=vi-wi。因此，ALE 算法中的控制方程可以表述為下面的質(zhì)量、動量以及能量守恒 方程：

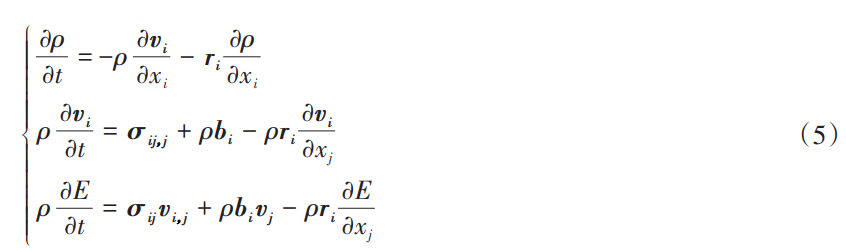
式中：bi為作用于流體上的體積力；σij，j = ∂σij/∂xj。其中σij為應(yīng)力張量分量，其表達式為：

式中：μd為動黏性系數(shù)；δij為Kronecker函數(shù)。

在進行流固耦合數(shù)值計算時，采用罰函數(shù)約束方式實現(xiàn)深海鈦合金耐壓結(jié)構(gòu)水下內(nèi)爆過程中的流固耦 合。通過在結(jié)構(gòu)積分耦合點尋找相應(yīng)的流體材料點，從而跟蹤主物質(zhì)（流體）表面和從物質(zhì)（結(jié)構(gòu)）節(jié)點的相 對位移l，根據(jù)l的大小來判斷是否引入界面力。若流體節(jié)點穿透結(jié)構(gòu)外表面，則界面力F就將施加到流體的 各節(jié)點上，其中F的大小與相對位移l成正比關(guān)系[32]：

式中：ki為基于主從節(jié)點質(zhì)量模型特性的剛度系數(shù)。

1.3　結(jié)構(gòu)材料本構(gòu)關(guān)系及失效模型

使用Johnson-Cook（ J-C）本構(gòu)模型來描述鈦合金TC4（ Ti-6Al-4V）球形耐壓殼的變形失效過程，該模型能用于描述大應(yīng)變、高應(yīng)變率、高溫環(huán)境下金屬材料的強度極限以及失效過程。J-C本構(gòu)模型[33]的主體由3部 分組成，分別表示等效塑性應(yīng)變、應(yīng)變率和溫度對流動應(yīng)力的影響：

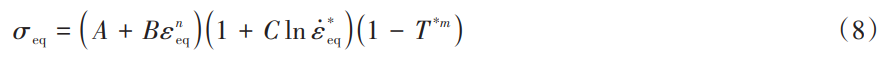
式中：σeq為等效應(yīng)力；εeq表示等效塑性應(yīng)變；ε* eq = εε0表示無量綱等效塑性應(yīng)變率，ε和 ε0分別表示塑性應(yīng) 變率和臨界應(yīng)變率；T* = (T - Tr) /(Tm - Tr)為無量綱化溫度，其中T為材料溫度，Tr為環(huán)境溫度，Tm為材料熔 點。其他參數(shù)說明以及具體數(shù)值見表1。

J-C失效模型[33]中斷裂應(yīng)變方程同樣由3部分組成：

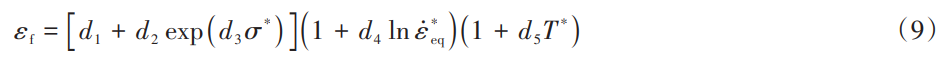
式中：εf為有效斷裂應(yīng)變；σ*=σH /σeq為應(yīng)力三軸度，σH為平均應(yīng)力；文中失效模型參數(shù)d1～d5分別取為−0.09、0.25、−0.5、0.014以及3.87[33]。

損傷參數(shù)D為一個積累量：

式中：Δεeq為一個積分循環(huán)的等效塑性應(yīng)變增量；εf為當前時間步有效斷裂應(yīng)變值。當D=1時單元被刪除。

2、水下內(nèi)爆流固耦合數(shù)值模型

2.1　數(shù)值模型

文中研究的鈦合金耐壓結(jié)構(gòu)為中空球形耐壓殼體，球殼內(nèi)徑 r0=0.25 m，外徑 R0=0.26 m，厚度 h=0.01 m。 計算域設(shè)置參考Zheng等[27]對鈦合金球內(nèi)爆的數(shù)值模擬和試驗研究，其中氣體域半徑與耐壓殼內(nèi)徑一致，水域外徑為氣體域半徑的15倍。在水域外邊界處設(shè)置無反射邊界條件，減少沖擊波在變邊界面反射后對計算結(jié)果的影響，從而等效深水環(huán)境下的無限水域。此外在水域外邊界面上施加向內(nèi)的均布載荷以維持內(nèi)部壓力，其大小和水域壓力一致，圖5為球形耐壓殼內(nèi)爆的計算域示意。

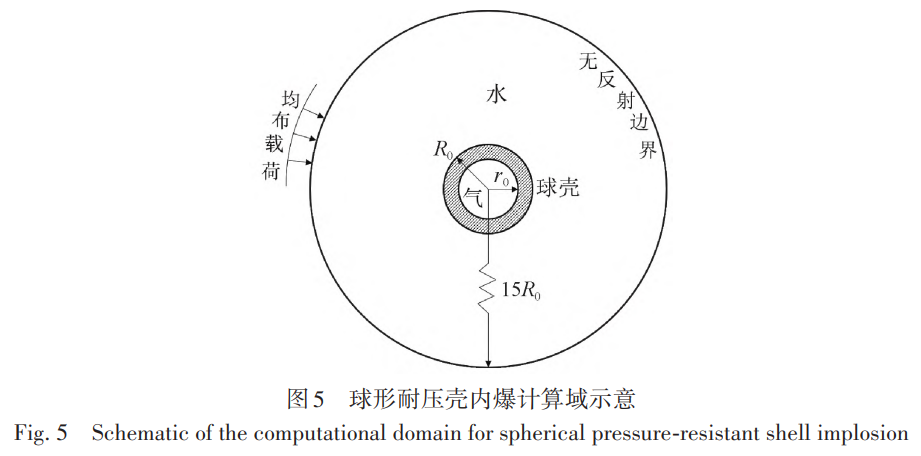
在進行內(nèi)爆流固耦合數(shù)值計算時，設(shè)置結(jié)構(gòu)域網(wǎng)格尺寸為5mm，空氣域網(wǎng)格尺寸為結(jié)構(gòu)域網(wǎng)格的2倍。 此外，為了滿足計算精度的需求并同時減少網(wǎng)格總量，水域采用漸變網(wǎng)格。其中水氣交界處網(wǎng)格尺寸和空 氣域一致，并沿球殼半徑向外膨脹，相鄰兩層網(wǎng)格尺寸的比例為1.08。壓力監(jiān)測點分別設(shè)置在球殼的x軸、y軸、z軸正方向，初始監(jiān)測點在球殼外表面處，之后每個監(jiān)測點之間距離為R0，每個方向各15個監(jiān)測點。水域 壓力為8 km超深海的靜水壓力，即80 MPa，其主要目的是開展超大深度環(huán)境下由于極限強度失效而導(dǎo)致的結(jié)構(gòu)破壞動態(tài)響應(yīng)機理研究，為中國大深度潛水器耐壓結(jié)構(gòu)開展前沿性的探索。

2.2　網(wǎng)格收斂性驗證

為了對計算結(jié)果的精確度進行判定，需要進行網(wǎng)格收斂性驗證。圖 6為粗、中、細 3種網(wǎng)格示意。其中 流體域初始網(wǎng)格尺寸的比例分別取為 2、1 和 2 /2，網(wǎng)格總量分別為 47 萬、116 萬和 312 萬。下文以P0=80 MPa水域壓力下內(nèi)徑r0=0.25 m的鈦合金耐壓球殼為考察對象，流體壓力和結(jié)構(gòu)變形的監(jiān)測點位置在z軸正向距球心0.26 m處（即球殼外表面位置處）。

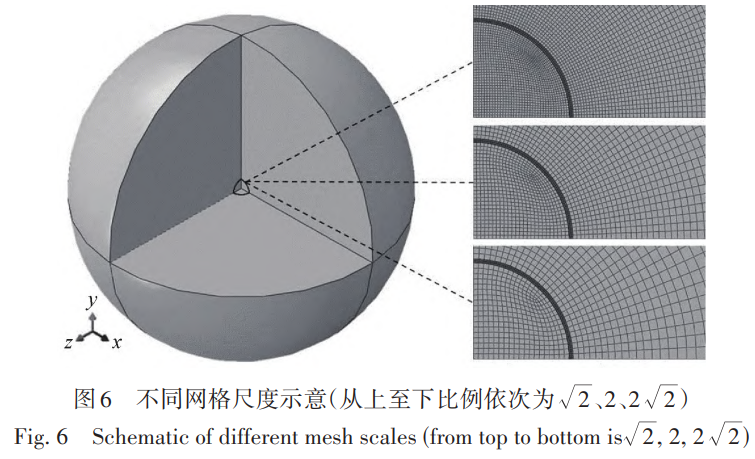
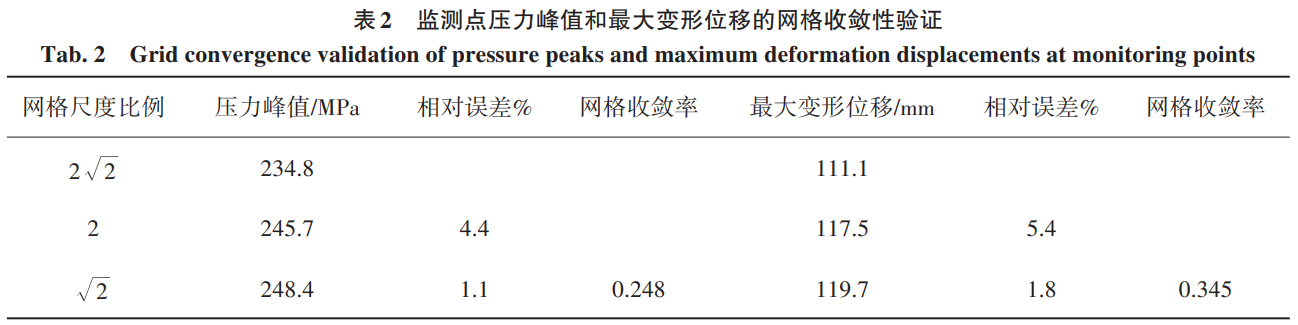
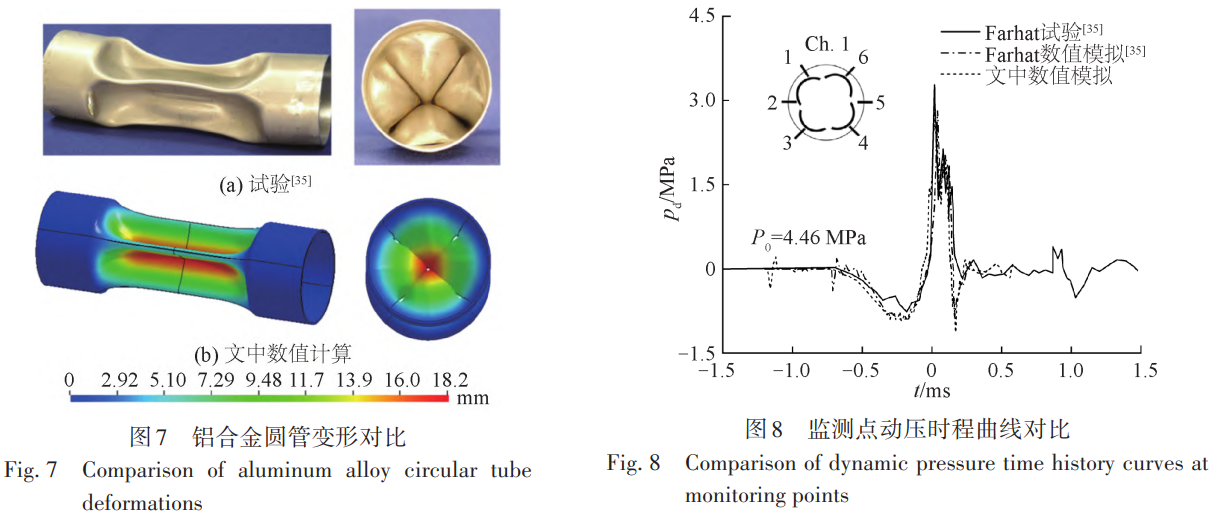
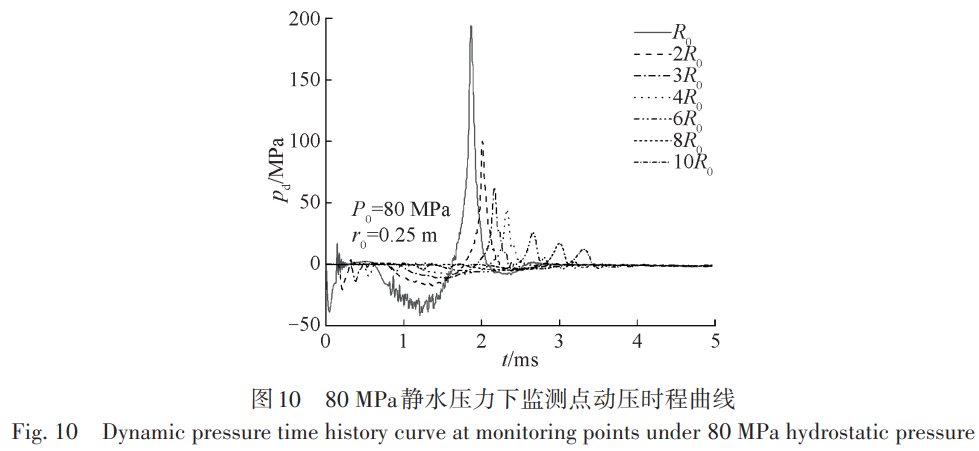
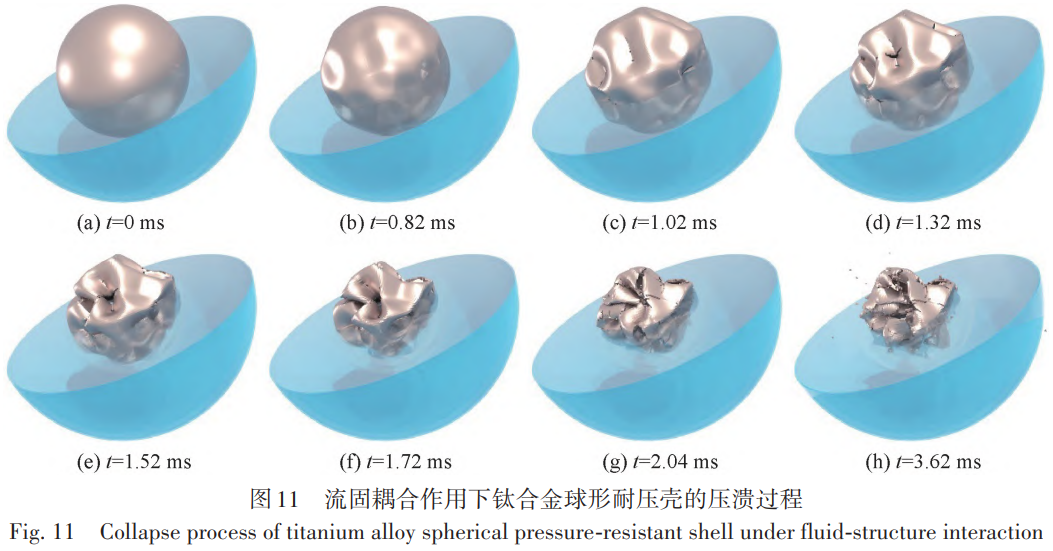
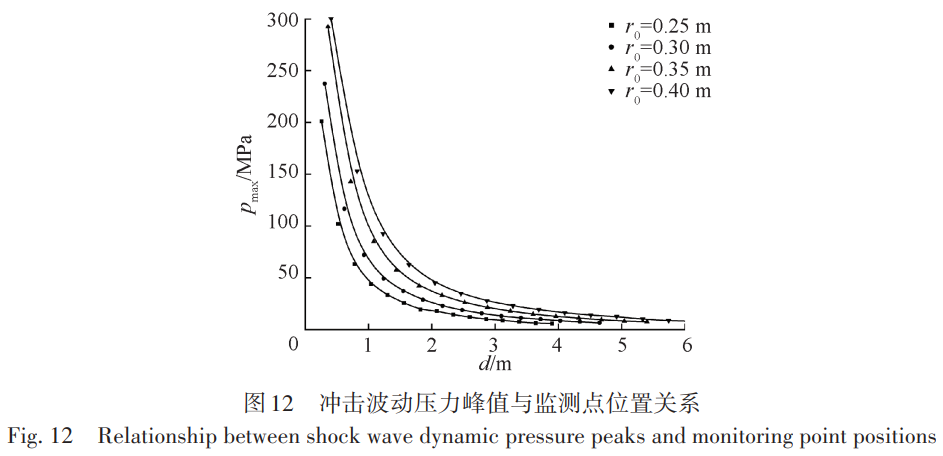
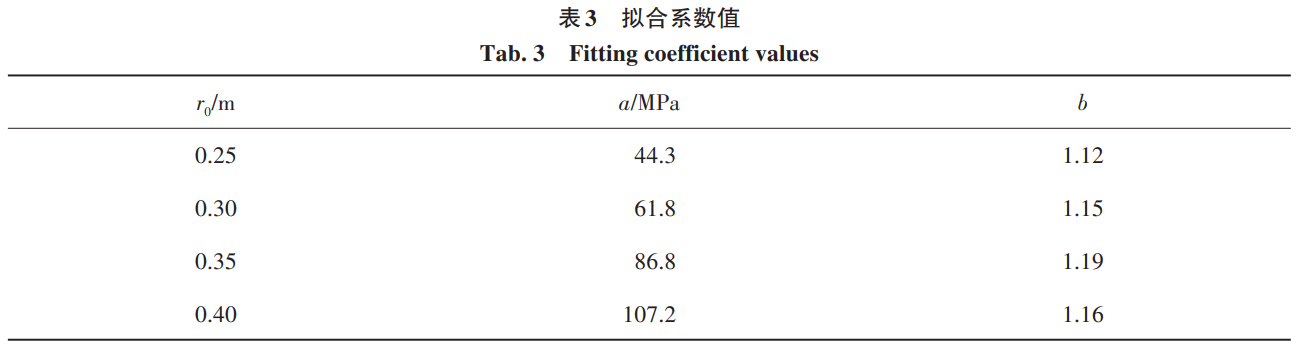
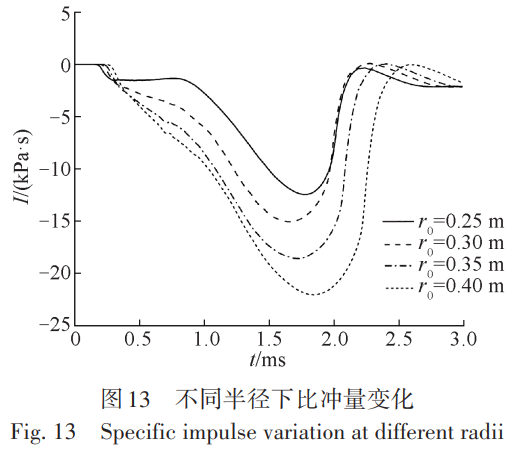
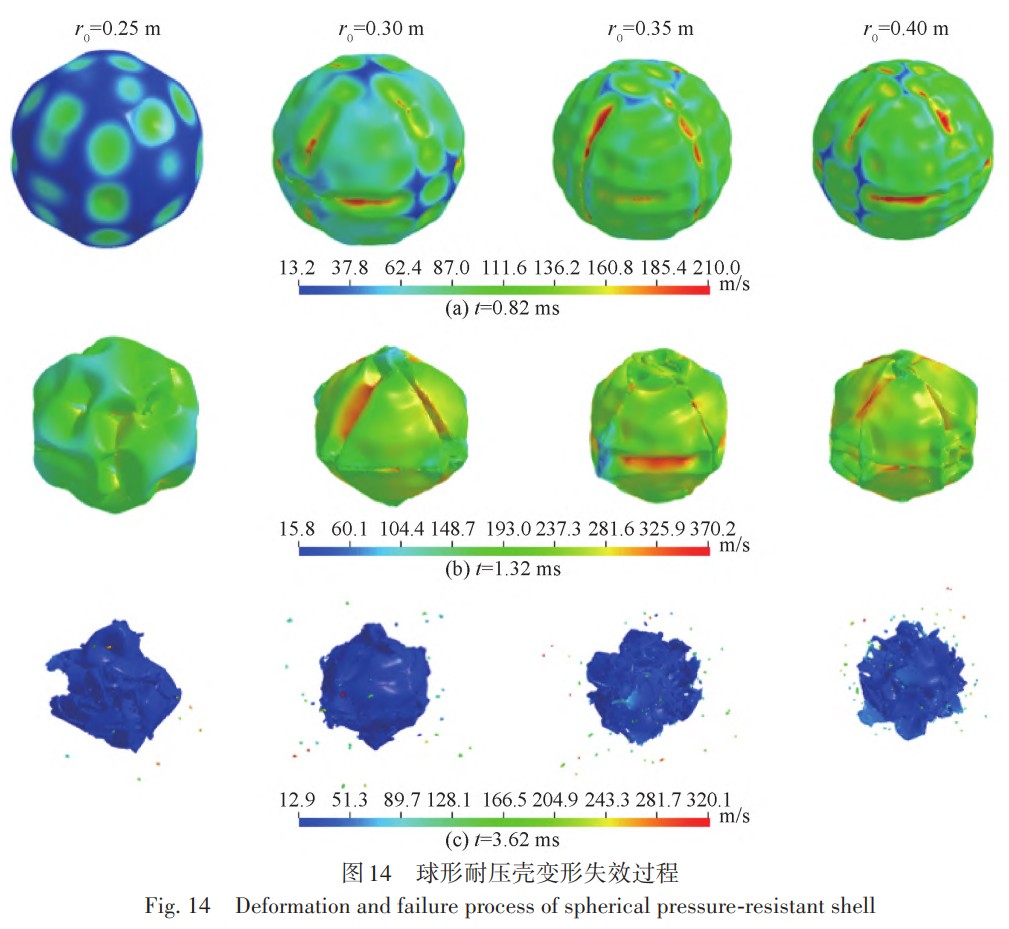
3種網(wǎng)格尺寸下的監(jiān)測點壓力峰值和最大變形位移結(jié)果如表2所示，其中壓力和位移的網(wǎng)格收斂率分別 為RG=0.248和RG=0.345，均滿足0

3、水下內(nèi)爆數(shù)值計算方法驗證

為了開展大深度海洋環(huán)境下鈦合金耐壓結(jié)構(gòu)內(nèi)爆流固耦合過程以及流場特性的研究，首先對數(shù)值計算 方法的準確性進行驗證，分別對比國外鋁合金圓管水下內(nèi)爆試驗和國內(nèi)鈦合金耐壓結(jié)構(gòu)準靜態(tài)壓潰試驗， 從耐壓結(jié)構(gòu)水下內(nèi)爆的流固耦合和結(jié)構(gòu)變形兩個方面進行數(shù)值計算方法的驗證。

3.1　鋁合金圓管水下內(nèi)爆試驗

首先以 Farhat等[35]的鋁合金圓管水下內(nèi)爆試驗為對照進行數(shù)值驗證。鋁合金圓管外徑 38.1 mm，厚度0.711 mm，長徑比 2。圓管網(wǎng)格尺寸 0.35 mm，歐拉域相鄰兩層網(wǎng)格膨脹比與上文耐壓球殼內(nèi)爆網(wǎng)格一致。 鋁合金采用雙線性彈塑性本構(gòu)模型，彈性模量和屈服應(yīng)力分別取為69.6 GPa、270 MPa，切線模量取0.274，不 考慮材料失效和單元刪除。圓管內(nèi)部壓力為一個標準大氣壓強即101.3 kPa，靜水載荷P0為4.46 MPa。

首先對比鋁合金圓管的結(jié)構(gòu)變形特征（圖7），文中數(shù)值計算結(jié)果的坍塌模式和最終變形形狀與試驗基 本一致。其次分析相同監(jiān)測點位置處的流體動壓p（d 實際水壓力和靜水壓力的差值）的時程曲線，見圖8，圖 中序號1~6為圓管內(nèi)爆試驗中不同監(jiān)測點方向，其中Ch. 1表示圖中曲線為1號點的沖擊波壓力。文中數(shù)值 計算結(jié)果與模型試驗和Farhat等[35]的數(shù)值計算結(jié)果得到的沖擊波曲線變化趨勢基本一致，三者的沖擊波壓 力。峰值分別為 3.11、3.28和 2.81 MPa，數(shù)值結(jié)果和試驗結(jié)果的相對誤差僅為 5.2%，相比于 Farhat等[35]的數(shù)值計算結(jié)果更為精確。文中數(shù)值計算結(jié)果與試驗存在誤差的主要原因可能有兩點：一是數(shù)值計算得到的壓 力是監(jiān)測點所在單元的平均壓力，而試驗中傳感器捕捉的是波陣面的壓力，由于波陣面的厚度遠小于流體 域的單元長度，同時監(jiān)測點實際位置處于計算單元的前半部分，導(dǎo)致壓力峰值偏小；二是試驗中鋁合金圓管 水下內(nèi)爆坍塌形態(tài)并非完全對稱，這可能導(dǎo)致內(nèi)爆沖擊波峰值不對稱分布，進而造成數(shù)值計算的沖擊波壓 力峰值偏小。

3.2　鈦合金耐壓結(jié)構(gòu)準靜態(tài)壓潰試驗

此外，為了進一步說明J-C本構(gòu)模型描述鈦合金材料耐壓球殼變形失效過程的準確性，對比了早期開展 的鈦合金耐壓球殼準靜態(tài)壓潰試驗[36]。試驗中將試件放入壓力筒，通過給試件表面緩慢加壓直至球殼壓 潰。試驗結(jié)果表明：該耐壓球殼的極限承載壓力為51 MPa，試驗后球殼的失效形態(tài)如圖9（a）所示。文中數(shù) 值計算得到的球殼極限強度為 51.6 MPa，相對誤差為 1.2%，出現(xiàn)該誤差的原因可能是球殼存在一定的制造 缺陷。數(shù)值計算得到的球殼失效形態(tài)如圖9（b）所示，可以看到數(shù)值計算和試驗中球殼的塌陷破壞都主要發(fā) 生在艙蓋局部加強處，球殼的主要破壞形式為剪應(yīng)力作用下的撕裂，同時加強部分整體和球殼分離。結(jié)果 表明：采用Johnson-Cook本構(gòu)模型能夠較為準確地描述鈦合金材料耐壓球殼坍塌和失效過程。

4、鈦合金耐壓結(jié)構(gòu)內(nèi)爆流固耦合過程及流場特性分析

為了探究鈦合金耐壓結(jié)構(gòu)內(nèi)爆流固耦合過程以及流場特性，首先對 2.1節(jié)中的鈦合金耐壓結(jié)構(gòu)模型開 展內(nèi)爆流固耦合過程研究；然后開展不同球殼半徑下的鈦合金耐壓球殼內(nèi)爆特性研究，分別設(shè)置球殼內(nèi)徑r0為0.25、0.30、0.35和0.40 m，球殼厚度h始終為0.01 m；最后研究不同水域壓力對內(nèi)爆特性的影響，分別設(shè)置 外界靜水壓力 P0為 80、90、100和 110 MPa，以探究超大深度下深海鈦合金耐壓結(jié)構(gòu)發(fā)生極限強度失效后的 毀傷特性。

4.1　鈦合金耐壓結(jié)構(gòu)內(nèi)爆流固耦合過程

以水域壓力 P0=80 MPa，球殼內(nèi)徑 r0=0.25 m，外徑 R0=0.26 m 為例，圖 10 為不同監(jiān)測點處的動壓時程曲 線。由圖 10 可知不同監(jiān)測點動壓變化趨勢基本相同。在監(jiān)測點 S=2R0處沖擊波時程可以分為以下 3 個階段。首先在t=0.15 ms左右出現(xiàn)一個歷時極短的壓降后迅速恢復(fù)到初始水壓，該壓降的產(chǎn)生實際上是歐拉域 在初始化時給結(jié)構(gòu)施加了突加載荷，導(dǎo)致結(jié)構(gòu)振動，在水介質(zhì)中形成稀疏波。然后從0.8 ms左右開始經(jīng)歷一 個持續(xù)時長約1 ms的低壓階段，1.4 ms左右降至最小值−17.5 MPa（−0.22P0）。該階段球殼被迅速壓潰，高壓 水流隨著結(jié)構(gòu)變形一起向球形耐壓殼內(nèi)部運動，導(dǎo)致球殼外部環(huán)境壓力下降并形成低壓區(qū)，因此沖擊波壓 力相對減小。同時，球形耐壓殼發(fā)生以彎曲變形為主的結(jié)構(gòu)動態(tài)響應(yīng)，并在外界水壓力的作用下持續(xù)變形 直至失效。最后當球殼被壓潰至極限狀態(tài)時，水繼續(xù)向內(nèi)運動，并在球殼中心位置附近相互碰撞，并由于 “水錘”效應(yīng)在球殼中心處產(chǎn)生局部高壓沖擊波，該沖擊波以球面波的形式向外傳遞。沖擊波到達該監(jiān)測點 時壓力呈指數(shù)形式升高，并在 2 ms左右達到壓力峰值 100 MPa （1.25P0），然后以指數(shù)形式下降至−4 MPa左 右，同時存在小幅度振蕩，直至逐漸回復(fù)至初始靜水壓力。

鈦合金球形耐壓殼的壓潰過程如圖11（水域半徑截取為2R0）所示。首先在靜水載荷的作用下球形耐壓 殼發(fā)生屈曲并逐漸產(chǎn)生非線性大變形，并在球殼表面表現(xiàn)為不規(guī)則凹陷。到t=1.02 ms，球殼出現(xiàn)破裂，同時 由于環(huán)境載荷的持續(xù)作用裂縫不斷擴大。球殼破裂后外部流體通過裂縫涌入其內(nèi)部，此時水動力載荷同時 作用于球殼內(nèi)外表面。t=2.04 ms時，球形耐壓殼部分內(nèi)壁面之間相互碰撞，球殼在結(jié)構(gòu)的相互作用力以及 水的沖擊下被撕裂成若干大片碎塊。鈦合金球形耐壓殼由于達到極限強度失效而發(fā)生內(nèi)爆時，結(jié)構(gòu)變形主 要以彎曲變形為主，且由于內(nèi)外流體載荷的壓差作用，彎曲變形主要朝球殼內(nèi)部方向運動。球殼被壓潰至 極限狀態(tài)時，大碎塊之間相互碰撞產(chǎn)生了大量小碎片，這些小碎片在高壓脈沖沖擊波壓力的作用下產(chǎn)生向 外的高速運動。

對于球形耐壓殼體，影響內(nèi)爆的主要因素包括球形耐壓殼的半徑以及外界水域壓力，在這兩者的影響 下，球形耐壓殼以不同的速度以及形狀坍塌，從而進一步影響水域中的沖擊波，下文主要就這兩方面影響進 行討論。

4.2　鈦合金耐壓結(jié)構(gòu)半徑變化對內(nèi)爆流場特性及結(jié)構(gòu)變形失效的影響

對于深潛器來說，較大的球形耐壓殼半徑可以在提供更大浮力的同時收納更多的非耐壓結(jié)構(gòu)，但是球 殼的承載能力會隨半徑的增大而減小，進而導(dǎo)致其安全性降低。為了進一步理解不同球殼半徑對內(nèi)爆的影 響，控制球殼厚度 h 為 0.01 m，水域壓力 P0為 80 MPa，球殼內(nèi)徑 r0分別取為 0.25、0.30，0.35 和 0.40 m 進行 計算。

不同球殼半徑下沖擊波動壓力峰值pmax隨監(jiān)測點距離d變化的趨勢如圖12所示。通過對各球殼半徑下動壓力峰值的分析，發(fā)現(xiàn)沖擊波壓力峰值隨距離的衰減可以用負指數(shù)冪函數(shù)p = ax-b擬合，其中a為常數(shù)系數(shù)，b為指數(shù)系數(shù)，不同球殼半徑下的擬合系數(shù)如表3所示。指數(shù)系數(shù)b隨球殼半徑增大先增大后減小，但均在1.1至1.2范圍內(nèi)。常數(shù)系數(shù)a隨球殼半徑增大逐漸增大。這是由于隨著球形耐壓殼半徑的增大，結(jié)構(gòu)發(fā)生失效后水向內(nèi)運動的距離也隨之增大，相對運動的流體在球中心位置附近發(fā)生碰撞產(chǎn)生的沖擊波脈動壓力也逐漸增大，因此在相同的環(huán)境載荷作用下，相同距離處的動壓力峰值隨著球殼半徑的增大而增大。但是隨著距離的增加，其增長率逐漸減小。

取監(jiān)測點S=2R0處沖擊波的超壓比沖量進行分析，如圖13所示。隨著球殼半徑增大，內(nèi)爆后比沖量最大 值Imax先增大后減小，但總體差距較小，各半徑下Imax最大差值小于0.45 kPa.s；比沖量最小值Imin逐漸減小，下降率分別為21%、23%、19%。取Imax和Imin的差值作為內(nèi)爆沖擊波比沖量峰值，由此可見球殼半徑主要通過改 變比沖量最小值來影響沖擊波強度。不同球殼半徑下監(jiān)測點S=2R0處的比沖量峰值隨著球殼半徑的增大而 增大，而且是關(guān)于球殼半徑的一次函數(shù)Imax - Imin = -4 681.1 + 66 636r（0 Pa.s）。

根據(jù)圖 11的結(jié)果，選取 t=0.82、1.32、3.62 ms這 3個典型時刻對不同半徑下的球殼失效變形進行對比分 析，如圖14所示。t=0.82 ms時刻球殼受到環(huán)境載荷作用呈高階失穩(wěn)模態(tài)形式向內(nèi)凹陷，這是球形耐壓殼在 高應(yīng)變率下坍塌時的非線性特征顯著的原因。球殼上不規(guī)則凹陷的數(shù)量隨著球殼半徑的增大而增加，r0= 0.25 m時，凹陷在球殼上的分布并無明顯規(guī)律，但隨著半徑增大，逐漸呈現(xiàn)三角形分布。t=1.32 ms時球殼出 現(xiàn)明顯裂縫，但相對內(nèi)壁面之間未發(fā)生碰撞，產(chǎn)生的碎塊面積較大且數(shù)量較少。裂縫形態(tài)和凹陷分布緊密 相關(guān)，r0=0.25 m 時，裂縫較短且分布零散，其他球殼半徑下有長裂縫產(chǎn)生且沿三角形凹陷分布。t=3.62 ms時，由于球殼內(nèi)壁面碰撞碎塊數(shù)量大幅增加，同時產(chǎn)生大量小面積碎片隨水流向外飛散。由圖14可見隨著 球殼半徑的增大，球殼塌陷后產(chǎn)生的碎塊和碎片數(shù)量增加，且在空間逐漸呈球體分布。盡管相同時刻下不 同半徑球殼的變形程度不同，但是在超高水壓載荷作用下，球殼均經(jīng)歷由彈塑性變形到失效的過程，同時先后生成大面積碎塊和小面積碎片。

4.3　深海環(huán)境壓力變化對內(nèi)爆流場特性及能量吸收的影響

隨著水深的增加，潛器承載的外界水壓力逐漸增加，研究不同水壓力下的內(nèi)爆現(xiàn)象可以為實際工程提 供參考。選取內(nèi)徑r0為0.25 m的耐壓球殼，將壓力P0分別設(shè)置為80、90、100、110 MPa進行計算。

不同水壓力下前5個監(jiān)測點的動壓力峰值如圖15所示。在一定水壓力下，壓力峰值的下降速率隨著監(jiān)測點距離的增大而顯著減小，符合指數(shù)衰減規(guī)律。各監(jiān)測點的壓力峰值隨初始水域壓力的增大而增大，且符合線性增長規(guī)律，將其進行擬合可以得到監(jiān)測點壓力峰值隨初始水壓的增長率分別為 2.56、1.09、0.67、0.43以及0.25。由此可見，隨著監(jiān)測點距離的增大，沖擊波峰值受初始水壓的影響逐漸減小。

同樣取監(jiān)測點S=2R0處的超壓比沖量進行分析，如圖16所示。比沖量峰值Imax隨靜水壓力增大而增大， 但總體差距較小，最大差值小于 0.25 kPa.s；比沖量谷值 Imin隨靜水壓力增大逐漸減小，下降率分別為 2.7%、3.1%、4.7%。比沖量峰、谷值之差與靜水壓力呈一次函數(shù)關(guān)系Imax - Imin = 7856.7 + 52.96P（0 Pa.s）。

不同初始壓力下水域的壓力場變化如圖17所示。

由圖17可知，鈦合金球形耐壓殼內(nèi)爆產(chǎn)生的沖擊波沿半徑向外傳播。這是因為球形耐壓殼在外界超高 水壓載荷下呈高階模態(tài)形式坍塌失穩(wěn)，因此外界靜水載荷呈球形向內(nèi)高速運動，在球心附近內(nèi)爆而產(chǎn)生球 形沖擊波，并向外圍低壓區(qū)均勻輻射。t=1 ms時，各工況下水域均處于負壓階段，水域中心部分壓力明顯小 于環(huán)境水壓，且在水域中存在明顯的低壓波。t=2 ms時，各工況下球殼均已被壓潰，內(nèi)爆沖擊波波面半徑隨 初始水域壓力增大而增大，分別約為 0.55、1.05、1.32、1.55 m。這是由于內(nèi)爆發(fā)生的時間隨水域壓力的增大而提前，低壓工況下球殼被壓潰時高壓工況中沖擊波已經(jīng)向外傳播了一定距離。對t=3 ms時各工況下的沖 擊波波面進行分析可知，沖擊波的波面壓力分別為 98.6、103.4、112.0、121.6 MPa，相對動壓力分別為 18.6、13.4、12.0、11.6 MPa，隨初始水壓力增大而減小且下降率逐漸減小。

鈦合金球形耐壓殼在高壓水載荷作用下發(fā)生內(nèi)爆時，水的內(nèi)能分別轉(zhuǎn)化為水的動能、空氣的內(nèi)能和動 能以及結(jié)構(gòu)的變形能和動能，內(nèi)爆過程中空氣和鈦合金球形耐壓殼都會吸收一部分能量，圖18為不同水壓 力下空氣和球殼的能量變化曲線。內(nèi)爆之前空氣內(nèi)能呈指數(shù)型增長，內(nèi)爆之后內(nèi)能急速下降并逐漸趨于平 穩(wěn)；對于球形耐壓殼，在球殼臨界失效之前其變形能呈線性增長，達到峰值后內(nèi)能下降，最后趨于平穩(wěn)。這 是因為球形耐壓殼在水壓力的作用下向內(nèi)壓潰時產(chǎn)生彎曲變形，結(jié)構(gòu)的變形能逐漸增大。此外，球形耐壓 殼應(yīng)變能極值早于空氣內(nèi)能極值，這說明球形耐壓殼內(nèi)爆坍塌過程中，球殼表面發(fā)生了局部斷裂，導(dǎo)致外界 高壓靜水載荷通過裂縫壓縮球殼內(nèi)部空氣，因此空氣的內(nèi)能呈現(xiàn)小幅度增長趨勢。然而隨著內(nèi)爆的演化， 球形耐壓殼完全坍塌，因此結(jié)構(gòu)變形能開始下降直至趨于定值。在此過程中，耐壓殼內(nèi)部空氣繼續(xù)被壓縮 至最小，然后開始膨脹，因此空氣內(nèi)能繼續(xù)增大到峰值后再減小。空氣最終內(nèi)能隨水域壓力的增加而增加， 球殼最終變形能隨初始水壓增加先增加后減少。相比于空氣內(nèi)能隨水域壓力的增加而明顯增加，球形耐壓 殼的變形能在 90 MPa 以上初始水域壓力下變化并不明顯。球殼吸收能量占二者總能量的比例依次為53.0%、52.3%、49.7%、47.9%，由此可見隨著初始水壓的增大，球殼吸能占比逐漸減小，但總體來說二者相差 較小。

5、結(jié)語

基于任意拉格朗日歐拉方法結(jié)合Johnson-Cook本構(gòu)和失效模型，對深海鈦合金耐壓結(jié)構(gòu)內(nèi)爆流固耦合 過程及毀傷特性開展研究。分析了鈦合金耐壓結(jié)構(gòu)內(nèi)爆時的流固耦合機制、結(jié)構(gòu)動態(tài)響應(yīng)及能量演化機 理，探究超大深度載荷下不同半徑和靜水壓力時鈦合金耐壓結(jié)構(gòu)極限強度失效破壞的物理機制。結(jié)論 如下：

1）鈦合金球形耐壓殼由于極限強度失效而發(fā)生內(nèi)爆時依次產(chǎn)生表面凹陷、裂縫擴展并最終破壞為大碎 塊和小碎片。

2）鈦合金球殼厚度一定時，沖擊波峰值隨靜水壓力的增大而線性增大，但增長率隨距離依次遞減；給定 半徑下沖擊波峰值隨距離的衰減服從負指數(shù)冪函數(shù)，衰減系數(shù)b均在1.1至1.2范圍內(nèi)。

3）鈦合金球形耐壓殼吸能占空氣和球殼吸收總能量的比例隨靜水壓力的增大而逐漸減小，但均維持在50%左右。

參 考 文 獻：

[1] 張洪彬， 徐會希 . 球柱殼耐壓艙體極限承載力研究[J]. 海洋工程， 2022， 40（2）： 154-161.

（ZHANG H B， XU H X. Research on the ultimate strength of spherical shell cover plus cylindrical shell pressure hulls[J]. The Ocean Engineering，2022， 40（2）： 154-161.（ in Chinese））

[2] 劉軍鵬， 于波， 張嘉毓， 等 . 大型球柱組合耐壓殼體結(jié)構(gòu)極限承載力模擬分析[J]. 中國海上油氣， 2020， 32（6）： 158-164.

（LIU J P， YU B， ZHANG J Y， et al. Simulation analysis of ultimate bearing capacity of large spherical-cylindrical combined pressure shell structur[J]. China Offshore Oil and Gas， 2020， 32（6）： 158-164.（ in Chinese））

[3] 劉濤 . 深海載人潛水器耐壓球殼設(shè)計特性分析[J]. 船舶力學(xué)， 2007， 11（2）： 214-220.

（LIU T. Research on the design of spherical pressure hull in manned deep-sea submersible[J]. Journal of Ship Mechanics， 2007， 11（2）： 214-220. （in Chinese））

[4] 王自力， 王仁華， 俞銘華， 等 . 初始缺陷對不同深度載人潛水器耐壓球殼極限承載力的影響[J]. 中國造船， 2007， 48（2）： 45-50.

（WANG Z L， WANG R H， YU M H， et al. The influence of the initial imperfections on the ultimate strength of manned deep-sea submersible pressure sphere hull[J]. Shipbuilding of China， 2007， 48（2）： 45-50.（ in Chinese））

[5] 于爽， 胡勇， 王芳， 等. 全海深載人潛水器超高強度鋼制載人球殼的極限強度分析與模型試驗[J]. 船舶力學(xué)， 2019， 23（1）： 51-57.

（YU S， HU Y， WANG F， et al. Ultimate strength analysis and model tests for full-ocean-depth manned cabin[J]. Journal of Ship Mechanics， 2019， 23（1）： 51-57.（ in Chinese））

[6] CRESSEY D. Ocean-diving robot Nereus will not be replaced[J]. Nature， 2015， 528（7581）： 176-177.

[7] WEI C Q， CHEN G， SERGEEV A， et al. Implosion of the Argentinian submarine ARA San Juan S-42 undersea： modeling and simulation[J]. Communications in Nonlinear Science and Numerical Simulation， 2020， 91： 105397.

[8] RAYLEIGH L. VIII. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. The London， Edinburgh， and Dublin Philosophical Magazine and Journal of Science， 1917， 34（200）： 94-98.

[9] PLESSET M S. The dynamics of cavitation bubbles[J]. Journal of Applied Mechanics， 1949， 16（3）： 277-282.

[10]KELLER J B， MIKSIS M. Bubble oscillations of large amplitude[J]. The Journal of the Acoustical Society of America， 1980， 68（2）： 628-633.

[11]ZHANG A M， LI S M， CUI P， et al. A unified theory for bubble dynamics[J]. Physics of Fluids， 2023， 35（3）： 033323.

[12]GILMORE F R. The growth or collapse of a spherical bubble in a viscous compressible liquid[M]. Pasadena， CA， USA： California Institute of Technology， 1952.

[13]TURNER S E. Small-scale implosion testing of glass and aluminum cylinders[J]. NUWC-NPT Technical Memorandum， 2004： 04-061.

[14]KENT R. Implosion research[J]. Sea Frame， 2008， 4（1）： 13-15.

[15]ZHU J， LUO M. Theoretical analysis and prediction of implosion during a high pressure test in GUSI-A1[R]. German： GKSS， 1983.

[16]朱繼懋， 羅曼蘆 . 用二相流理論進行承壓試驗的內(nèi)破裂問題的預(yù)報[J]. 海洋工程， 1985， 3（1）： 1-14.

（ZHU J M， LUO M L. Calculation prediction of implosion with the two-phase flow theory in a high pressure test[J]. The Ocean Engineering， 1985， 3（1）： 1-14.（ in Chinese））

[17]陳建國， DIETRICH R A， 朱繼懋 . 內(nèi)破裂的數(shù)值模擬與分析[J]. 中國造船， 1994（3）：83-92.

（CHEN J G， DIETRICH R A， ZHU J M. Numerical simulation and analysis of implosion phenomena[J]. Shipbuilding of China， 1994（3）：83-92. （ in Chinese））

[18]陳建國， DIETRICH R A， 朱繼懋 . 影響內(nèi)破裂因素的數(shù)值分析研究[J]. 海洋工程， 1994， 12（2）：13-25.

（CHEN J G， DIETRICH R A， ZHU J M. Numerical analysis of factors influencing implosion[J]. The Ocean Engineering， 1994， 12（2）：13-25.（ in Chinese））

[19]ZHANG X L， FENG M L， ZHAO M， et al. Failure of silicon nitride ceramic flotation spheres at critical state of implosion[J]. Applied Ocean Research， 2020， 97： 102080.

[20]SUN S X， ZHAO M. Numerical simulation and analysis of the chain-reaction implosions of multi-spherical hollow ceramic pressure hulls in deep-sea environment[J]. Ocean Engineering， 2023， 277： 114247.[21]SUN S X， ZHAO M， JIANG Y T. Numerical study of chain-reaction implosions in a spatial array of ceramic pressure hulls in the deep sea using a compressible multiphase flow model[J]. Physics of Fluids， 2024， 36（1）： 016112.

[22]HU Y D， ZHAO Y F， ZHAO M， et al. Three phases fluid-structure interactive simulations of the deepsea ceramic sphere’s failure and underwater implosion[J]. Ocean Engineering， 2022， 245： 110494.

[23]GISH L A， WIERZBICKI T. Estimation of the underwater implosion pulse from cylindrical metal shells[J]. International Journal of Impact Engineering， 2015， 77： 166-175.

[24]TURNER S E. Underwater implosion of glass spheres[J]. The Journal of the Acoustical Society of America， 2007， 121（2）：844-852.

[25]TURNER S E， AMBRICO J M. Underwater implosion of cylindrical metal tubes[J]. Journal of Applied Mechanics， 2013， 80（1）： 011013.

[26]GUPTA S， MATOS H， SHUKLA A， et al. Pressure signature and evaluation of hammer pulses during underwater implosion in confining environments[J]. The Journal of the Acoustical Society of America， 2016， 140（2）： 1012-1022.

[27]ZHENG J C， HE Y P， ZHAO M， et al. Dynamic response analysis of spherical pressure hull implosion inside adjacent underwater structure[J]. Ocean Engineering， 2023， 283： 115169.

[28]ZHENG J C， ZHAO M. Fluid-structure interaction of spherical pressure hull implosion in deep-sea pressure： experimental and numerical investigation[J]. Ocean Engineering， 2024， 291： 116378.

[29]常輝， 董月成， 淡振華， 等 . 我國海洋工程用鈦合金現(xiàn)狀和發(fā)展趨勢[J]. 中國材料進展， 2020， 39（增刊 1）： 585-590.

（CHANG H， DONG Y C， DAN Z H， et al. Current status and development trend of titanium alloy for marine engineering in China [J]. Materials China， 2020， 39（Suppl1）： 585-590.（ in Chinese））

[30]KWON Y W， SUGIMOTO S. Numerical study of implosion of shell structures[J]. Multiscale and Multidisciplinary Modeling， Experiments and Design， 2020， 3（4）： 313-336.

[31]門建兵， 蔣建偉， 王樹有. 爆炸沖擊數(shù)值模擬技術(shù)基礎(chǔ)[M]. 北京： 北京理工大學(xué)出版社， 2015.

（MEN J B， JIANG J W， WANG S Y. Fundamentals of numerical simulation for explosion and shock problems[M]. Beijing： Beijing Insititute of Technology Press， 2015.（ in Chinese））

[32]HALLQUIST J O， GOUDREAU G L， BENSON D J. Sliding interfaces with contact-impact in large-scale Lagrangian computations[J]. Computer Methods in Applied Mechanics and Engineering， 1985， 51（1/2/3）： 107-137.

[33]LESUER D. Experimental investigations of material models for Ti-6A1-4V and 2024-T3[R]. Livermore， CA （United States）： Lawrence Livermore National Lab.（LLNL）， 1999.

[34]ITTC. Uncertainty analysis in CFD， uncertainty assessment methodology[C]//Proceedings of the International Towing Tank Conference.[ S. l. ： s. n.]， 1999： 4. 9-04-01-01.

[35]FARHAT C， WANG K G， MAIN A， et al. Dynamic implosion of underwater cylindrical shells： experiments and computations[J]. International Journal of Solids and Structures， 2013， 50（19）： 2943-2961.

[36]WU Y， DING J， WANG F， et al. Research on the quasi-static collapse and instantaneous implosion of the deep-sea spherical pressure hull[J]. Marine Structures， 2022， 83： 103191.

---

tag標簽:深海鈦合金

---